Question

Two fair six-sided dice are tossed independently. Let M be the maximum of two tosses. What is the probability mass function of M? a) 1/6 b) 5/36 c) 11/36 d) 1/3

Answer 1

The probability mass function of the maximum value, M, when two fair six-sided dice are tossed is found by calculating the probability of each possible maximum value. The correct answer for the maximum value of 6 is c) 11/36.

Step-by-step explanation:

The student is asking for the probability mass function of the maximum value, M, when two fair six-sided dice are tossed independently. To find the probability mass function of M, we consider all possible outcomes when the dice are rolled. Since there are 6 sides on each die, there are a total of 6 x 6 = 36 possible outcomes.

Here is how you would calculate the probability for each possible maximum value M from 1 to 6:

• For M=1, the only outcome is (1,1), so P(M=1) = 1/36.
• For M=2, the outcomes are (1,2), (2,1), and (2,2), so P(M=2) = 3/36 = 1/12.
• For M=3, considering similar combinations, P(M=3) = 5/36.
• For M=4, P(M=4) = 7/36.
• For M=5, P(M=5) = 9/36.
• For M=6, the maximum, P(M=6) includes all outcomes where at least one die shows a 6, so P(M=6) = 11/36.

Therefore, the correct answer to the question is c) 11/36, which is the probability of the maximum of two dice rolls being 6.

Answer 2

The correct answer to the question "What is the probability mass function of
`\( M \)`?" is not simply one of the options a), b), c), or d), but the set of probabilities we calculated for each value of
`\( M \)`. The probability for
`\( M = 6 \)`, which is the highest possible maximum value, is
`\( (11)/(36) \)`, corresponding to option c).

The probability mass function (PMF) of a random variable gives the probability that a random variable is exactly equal to some value. In the case of two six-sided dice tossed independently, the maximum value
`\( M \)` that can be observed from the two tosses can range from 1 to 6.

To find the PMF of
`\( M \),` we need to calculate the probability that the maximum of the two dice is each of the possible values from 1 to 6.

For
`\( M = 1 \)`, both dice must show 1. There is only one outcome for this:

- Probability
`\( P(M=1) = \left((1)/(6)\right) * \left((1)/(6)\right) = (1)/(36) \)`.

For
`\( M = 2 \)`, the outcomes can be (1,2), (2,1), or (2,2), but not (1,1) as we've already accounted for that in
`\( M = 1 \)`:

- Probability
`\( P(M=2) = 3 * \left((1)/(6)\right) * \left((1)/(6)\right) = (3)/(36) \)`.

Similarly, for
`\( M = 3 \)`, the outcomes can be (1,3), (2,3), (3,1), (3,2), or (3,3), but not any with maximum 2 or less:

- Probability
`\( P(M=3) = 5 * \left((1)/(6)\right) * \left((1)/(6)\right) = (5)/(36) \).`

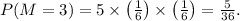
Following this pattern, we can find the probabilities for \( M \) from 4 to 6.

For \( M = 4 \), there are 7 outcomes: (1,4), (2,4), (3,4), (4,1), (4,2), (4,3), and (4,4). None of these include the previous maximum values.

- Probability
`\( P(M=4) = 7 * \left((1)/(6)\right) * \left((1)/(6)\right) = (7)/(36) \).`

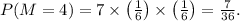
For \( M = 5 \), there are 9 outcomes: (1,5), (2,5), (3,5), (4,5), (5,1), (5,2), (5,3), (5,4), and (5,5).

- Probability
`\( P(M=5) = 9 * \left((1)/(6)\right) * \left((1)/(6)\right) = (9)/(36) \).`

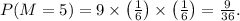
Finally, for \( M = 6 \), there are 11 outcomes: (1,6), (2,6), (3,6), (4,6), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), and (6,6).

- Probability
`\( P(M=6) = 11 * \left((1)/(6)\right) * \left((1)/(6)\right) = (11)/(36) \).`

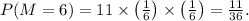
Therefore, the PMF of
`\( M \)` is as follows:

-
`\( P(M=1) = (1)/(36) \)`

-
`\( P(M=2) = (3)/(36) \)`

-
`\( P(M=3) = (5)/(36) \)`

-
`\( P(M=4) = (7)/(36) \)`

-
`\( P(M=5) = (9)/(36) \)`

-
`\( P(M=6) = (11)/(36) \)`

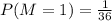
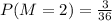
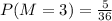
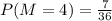
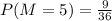
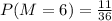
The correct answer to the question "What is the probability mass function of
`\( M \)`?" is not simply one of the options a), b), c), or d), but the set of probabilities we calculated for each value of
`\( M \)`. The probability for
`\( M = 6 \)`, which is the highest possible maximum value, is
`\( (11)/(36) \)`, corresponding to option c).