Question

Three squares are shown. Find the area of the square made from side AC.

Answer 1

Answer: 196 becuase line AC is 14

Explanation:

We have one angle of 90, which means the rest of the angles are 45. (90+45+45 = 180)

This also means that the length of AC and BC are both the same

We also know that the shape is a square meaning all sides are the same

We also know the Area of the square is 196

If area is base times height and a square has the same length for the base as height, then we know the formula is A x A=196 or A^2=196. So take the reverse of 196 by square rooting it.

`√(196) = 14`

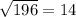
So, line BC equals 14

Now remember how I said Line BC and AC are the same length. Well because of that AC is also 14. Lastly, because the shape is a square all sides are 14, meaning the square from the line AC is
`14^(2)` or 196.

Answer 2

Check the picture below.

`\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies a=√(c^2 - o^2) \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{BC}\\ a=\stackrel{adjacent}{AC}\\ o=\stackrel{opposite}{6.7} \end{cases} \\\\\\ AC=√( BC^2 - AB^2)\implies AC=√( 196 - 6.7^2 ) \\\\\\ AC=√(196-44.89)\implies AC=√( 151.11 )\implies AC\approx 12.29`