Question

the highest temperature ever recorded in the united states was 56.7 C (134 F). what was the speed of the oxygen molecules in the air that day?

Answer 1

507 m/s

Step-by-step explanation:

To determine the speed of oxygen molecules in the air at a temperature of 56.7 °C (134 °F), we use the root mean square speed formula for gas molecules.. The formula for the average speed of gas molecules is given by:

`v_(rms)=\sqrt{(3RT)/(M)}`

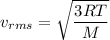
Where,

• 'v' is the average speed of the molecules

• 'R' is the gas constant (≈ 8.31 J/mol·K)

• 'T' is the absolute temperature in Kelvin,

• 'M' is the molecular mass of the gas.

We are given,

• T = 56.7 °C (56.7 + 273.15 = 329.85 K)
• M = 2(15.999 g/mol) = 31.998 g/mol O₂ (this will need to be converted to kg/mol)

Plug our given values into the formula:

`\Longrightarrow v_(rms) =\sqrt{(3(8.31 \ (J)/(mol \cdot K) )(329.85 \ K))/(\Big((31.998 \ g)/(1 \ mol)* (1 \ kg)/(1000 \ g) \Big))}\\\\\\\\\Longrightarrow v_(rms) =\sqrt{(3(8.31 \ (J)/(mol \cdot K) )(329.85 \ K))/((0.031998 \ (kg)/(mol)))}\\\\\\\\\Longrightarrow v_(rms)=\sqrt{256990 \ (m^2)/(s^2) }\\\\\\\\\therefore v_(rms) \approx \boxed{507 \ m/s}`

Thus, we get a speed of approximately 507 m/s.