Question

Suppose that the height H of a Ferris wheel can be modeled by the function n H(t)= -16cos(t/45)+24, where t is the time in seconds. What is the maximum height of a cabin? Use 3.14 for π

Answer 1

40 feet.

Explanation:

The height of the Ferris Wheel is modeled by:

`\displaystyle H(t)=-16\cos\Big((t)/(45)\Big)+24`

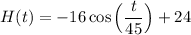
Where H(t) is the height (in feet (assuming)) and t is the time in seconds.

Remember that the value of cosine, regardless of the input, will always be between -1 and 1. That is:

`-1\leq \cos(t)\leq 1`

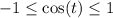
So, we can use the two maximums. Testing -1 and 1, we get:

`H(t)=-16(1)+24=8`

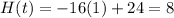
And:

`H(t)=-16(-1)+24=40`

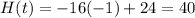
Therefore, the maximum height of a cabin of the Ferris Wheel will be 40 feet in the air.

Notes:

And the minimum height will be 8 feet.

We are not asked to find t. To do so, however, set H(t) = 40 and find the general solution for t.