Answer:
a) Yes, triangles JNM and JLK are similar by the AA Similarity Postulate
b) JN = 4 in
c) LN = 1.5 in
JK = 3.5 in
d) Area ratio = 2.56 : 1
Step-by-step explanation:
Given:
KL = 5 in
MN = 8 in
JL = 2.5 in
MK = 2.1 in
From triangle JLK and JNM, we can deduce the following;

a) The AA Similarity theorem states that if two pairs of corresponding angles in two triangles are congruent, then the two triangles are similar. From the above, we can see that we have two pairs of corresponding angles that are congruent, so we can say that triangles JLK and JNM are similar.
b) Note that, in similar triangles, corresponding sides are equal in proportion.
So we can go ahead and solve for JN as seen below;
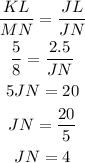
So JN is 4 in
c)
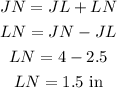
So LN is 1.5 in
Let's find the length of JK;

So the length of JK is 3.5 in
d) The area ratio of two similar triangles is equal to the square of the ratio of any two corresponding sides.
So the ratio of triangle JNM to JKL is;
