Question

Find the length of cubical box where base is 100cm²​

Answer 1

So we know the base of a cubical box is a square

Area Of Square = side^2

so 100 = s^2

s = ±10

but the side can't be negative, so the side is 10cm

and the length of a cube is the same as the side of the square's side,

so l = 10cm

Answer 2

Length = 10cm

Explanation:

The base area of a cube is given by the formula
`\sf \textsf{Area} = s^2`, where
`\sf s` is the length of one side of the cube.

In this case, we've the base area (
`\sf \textsf{Area}`) is
`\sf 100 \ \textsf{cm}^2`.

So, we can set up the equation:

`\sf s^2 = 100`

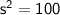
Now, solve for
`\sf s`:

`\sf s = √(100)`

`\sf s = 10`

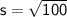
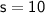
Therefore, the length of one side of the cube is
`\sf 10 \ \textsf{cm}`.

Since all sides of a cube are equal, the length of the cubical box is
`\sf 10 \ \textsf{cm}`.