The graphs below are exponential function graphs, the general formular takes the form
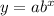
The graph of
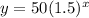
Is shown below
The graph of
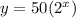
Is shown below
The graph of
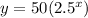
Is shown below
Hence,
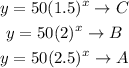
The equation of the exponential function is
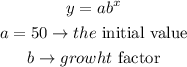
Thus the higher the growth factor the greater the rate of attaining a higher value within a short period.
That is why you see that the function with growth factor of 2.5 grows faster than that of 2 and also 1.5.
So the at x value of 3, the function with the greatest growth factor will have the highest y-value.
This implies , growth factor of 2.5 will have the highest, that corresponds to graph with colour green. Function with growth factor 2 will be the next to that of 2.5, that is red colored graph, and the last will be blue.