Question

Reducción de la ecuación general a la ecuación ordinaria

x² + y² + 5y - 1 = 0.​

Answer 1

The equations that represent the reduction of the given general equation to the ordinary equation in terms of x and y are;

`y + 2.5 = \±\sqrt(7.25 - x^2)\\y = -2.5 \± \sqrt(7.25 - x^2)`

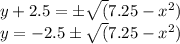
How to reduce the general equation to ordinary equation

To reduce the general equation
`x^2 + y^2 + 5y - 1 = 0` to the ordinary equation, complete the square for the variable

Starting with the equation:

`x^2 + y^2 + 5y - 1 = 0`

Rearrange terms involving y together:

`y^2 + 5y = 1 - x^2`

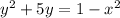
Now, complete the square for the y terms by adding and subtracting
`(5/2)^2` = 6.25:

`y^2 + 5y + 6.25 - 6.25 = 1 - x^2`

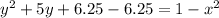
Factor the perfect square trinomial:

`(y + 2.5)^2 - 6.25 = 1 - x^2`

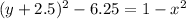
Rearrange the equation to isolate the perfect square:

`(y + 2.5)^2 = 1 - x^2 + 6.25\\(y + 2.5)^2 = 7.25 - x^2`

Finally, take the square root of both sides to solve for y:

`y + 2.5 = \±\sqrt(7.25 - x^2)\\y = -2.5 \± \sqrt(7.25 - x^2)`

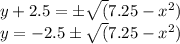
This equation represents the reduction of the given general equation to the ordinary equation in terms of x and y.