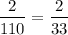Question

Kerry has a box of chocolates which are all flavoured with either mint or toffee. The possible outcomes of Kerry picking two chocolates at random are shown in the tree diagram below. If both chocolates are the same flavour, what is the probability that they are both toffee? Give your answer as a fraction in its simplest form.

​

Answer 1

The probability is 3/28.

Explanation:

All you have to do is multiply the first outcome of toffee ( 3/8 ) by the second outcome of toffee ( 2/7 ).

3/8 x 2/7 = 6/56 which can be simplified to 3/28.

Therefore, the probability of picking two toffee flavoured chocolates is 3/28.

Answer 2

The probability of Kerry picking two toffees is
`$(2)/(110) = (2)/(33)$`

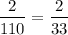
The probability of Kerry picking two toffees is the probability of picking a toffee, then another toffee, which can be found by multiplying the probability of picking a toffee on the first pick by the probability of picking another toffee on the second pick, given that the first chocolate was a toffee.

From the tree diagram, we can see that the probability of picking a toffee on the first pick is
`$(2)/(11)$` and the probability of picking another toffee on the second pick, given that the first chocolate was a toffee, is
`$(1)/(3)$` (because there is only one toffee left, and there are three chocolates remaining altogether).

Therefore, the probability of Kerry picking two toffees is
`$(2)/(11) * (1)/(3) = (2)/(33)$`.

Alternatively, we could note that there are a total of
`$11 * 10 = 110$` equally likely outcomes, of which 2 result in Kerry picking two toffees.

The probability of Kerry picking two toffees is
`$(2)/(110) = (2)/(33)$`