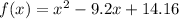Question

PLEASE HELP ME!!!! ITS ALGEBRA 2 ILL GIVE POINTS

Answer 1

The polynomial function f(x) with the given conditions is:

`f(x) = x^2 - 9.2x + 14.16`

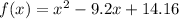
How to find a polynomial function

To find a polynomial function f(x) with rational coefficients, a leading coefficient of 1, and the given zero 4.6 - √7, use the concept of conjugate pairs.

Since the given zero is not rational, its conjugate, 4.6 + √7, will also be a zero of the polynomial.

To find the polynomial function, multiply the factors corresponding to the zeros.

Thus, we have:

`f(x) = (x - (4.6 - \sqrt7))(x - (4.6 + \sqrt7))`

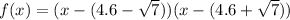
Expand this expression

`f(x) = (x - 4.6 + \sqrt7)(x - 4.6 - \sqrt7)`

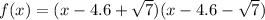
Using the difference of squares, simplify further:

`f(x) = ((x - 4.6)^2 - (\sqrt7)^2)`

Simplifying the expression inside the parentheses, we have:

`f(x) = (x - 4.6)^2 - 7`

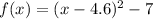
By expanding and rearranging, the polynomial function in standard form is:

`f(x) = x^2 - 9.2x + 21.16 - 7`

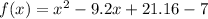
Simplifying the constant terms

`f(x) = x^2 - 9.2x + 14.16`

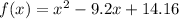
Therefore, the polynomial function f(x) with the given conditions is:

`f(x) = x^2 - 9.2x + 14.16`