Question

Graph the solution set of this inequality:

5x − 4y > 20.

Answer 1

See below

Explanation:

To graph the solution set of the inequality
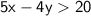`\sf 5x - 4y > 20`, we'll first rewrite it in slope-intercept form (
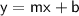`\sf y = mx + b`), where
`\sf m` is the slope and
`\sf b` is the y-intercept.

`\sf 5x - 4y > 20`

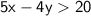
Subtract
`\sf 5x` from both sides:

`\sf 5x - 4y -5x> -5x20`

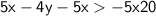
[tex]\sf -4y > -5x + 20[/tex]

Divide both sides by
`\sf -4` (note that when dividing by a negative number, the inequality sign flips):

`\sf y < (5)/(4)x - 5`

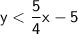
Now, we can graph the corresponding line
`\sf y = (5)/(4)x - 5` and shade the region below it because we have
`\sf y < (5)/(4)x - 5`.

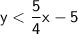Here's how we can graph it:

1. Plot the y-intercept at
`\sf y = -5`. This gives us the point (0, -5).

2. Use the slope
`\sf (5)/(4)` to find another point. For example, move up 5 units and to the right 4 units from the y-intercept, giving we the point (4, 0).

3. Draw a dashed line through these two points.

Now, since we have
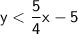`\sf y < (5)/(4)x - 5`, shade the region below the line.

The shaded region represents the solution set of the inequality
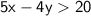`\sf 5x - 4y > 20`.