Question

What is y=4/5x + 2 written in standard form?

Answer 1

4x - 5y = -10

Explanation:

The standard form of a linear equation is

ax + by = c

Start with y = 4/5 x + 2.

Multiply both sides by 5 to get rid of the denominator.

5y = 4x + 10

Now subtract 5y from both sides.

0 = 4x - 5y + 10

Subtract 10 from both sides.

-10 = 4x - 5y

Switch sides.

4x - 5y = -10

Answer 2

`\sf 4x - 5y = -10`

Explanation:

The standard form of a linear equation is usually written as:

`\sf Ax + By = C`

where
`\sf A`,
`\sf B`, and
`\sf C` are integers, and
`\sf A` is positive.

The given equation is
`\sf y = (4)/(5)x + 2`.

To write it in standard form, we can move all terms to one side of the equation and ensure that the coefficients
`\sf A`,
`\sf B`, and
`\sf C` are integers:

`\sf -(4)/(5)x + y = 2`

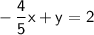
To eliminate the fraction, multiply through by 5 to clear the fraction:

`\sf -4x + 5y = 10`

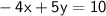
Now, to make the coefficient of
`\sf x` positive, multiply through by -1:

`\sf 4x - 5y = -10`

So, the equation
`\sf y = (4)/(5)x + 2` written in standard form is
`\sf 4x - 5y = -10`.