Question

The product of 7y and 7x when the smallest number is y

Answer 1

The product of (x + 7y) and (7x - y) is
`7x^2 - 7y^2 + 48xy`.

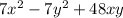How to find the product of the expressions

To find the product of the expressions (x + 7y) and (7x - y), use the distributive property.

Multiply each term in the first expression by each term in the second expression and then combine like terms, if any.

`(x + 7y)(7x - y)` can be expanded as follows:

`(x)(7x) + (x)(-y) + (7y)(7x) + (7y)(-y)`

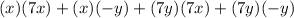
Simplifying each term:

`7x^2 - xy + 49xy - 7y^2`

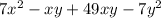
Combining like terms:

`7x^2 + 48xy - 7y^2`

It can be rearranged thus;

`7x^2 - 7y^2 + 48xy`

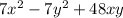
Therefore, the product of (x + 7y) and (7x - y) is
`7x^2 - 7y^2 + 48xy`.

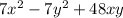Find the complete question below;

Find the product (x + 7y) and (7x - y)

a. 7x^2 - 7y^2 + 48xy

b. 6x^2 - 7y^2 + 48xy

c. 7x^2 - 7y^2 + 49xy

d. 6x^2 - 7y^2 + 49xy