Answer:
The coefficient of
 term :
term :
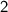
The coefficient of
 term :
term :

Explanation:
To find the coefficients of
 and
and
 in the product
in the product
 , let's first perform the multiplication:
, let's first perform the multiplication:
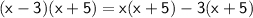
Now, distribute the terms:
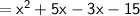
Combine like terms:
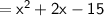
Now, we can identify the coefficients:
- The coefficient of
 term is
term is
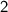 .
. - The coefficient of
 term is
term is
 .
.
Therefore, in the expression
 , the coefficient of the
, the coefficient of the
 term is
term is
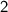 and the coefficient of the
and the coefficient of the
 term is
term is
 .
.