Question

Plot the po∫ given in polar coordinates. [ (-8, {2pi}{3}) ] and then find three additional polar representations of the po∫ using ( -2π). a) ( (8, {4pi}{3}) ), ( (-8, -{4pi}{3}) ), ( (8, -{8pi}{3}) ) b) ( (-8, {4pi}{3}) ), ( (8, -{4pi}{3}) ), ( (-8, -{8pi}{3}) ) c) ( (8, -{2pi}{3}) ), ( (-8, {2pi}{3}) ), ( (8, {4pi}{3}) ) d) ( (-8, -{2pi}{3}) ), ( (8, {2pi}{3}) ), ( (-8, {8pi}{3}) )

Answer 1

The three additional polar representations of the po∫
`( (8, -{2π}{3}) ), ( (-8, {2π}{3}) ), ( (8, {4π}{3}) )`. Thus the correct option is c.

Step-by-step explanation:

In polar coordinates, a point is represented by its distance from the origin (r) and the angle it makes with the positive x-axis (θ). For the given point
`(-8, {2π}{3})`, the distance is 8 units, and the angle is {2π}{3} radians. To find three additional polar representations using (-2π), we add (-2π) to the original angle:

1. Adding (-2π) to {2π}{3} gives {4π}{3}, so the first representation is
`(8, -{2π}{3}).`

2. Adding (-2π) again gives -{4π}{3}, so the second representation is
`(-8, {2π}{3}).`

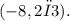
3. Adding (-2π) once more gives {4π}{3}, so the third representation is
`(8, {4π}{3}).`

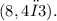
Therefore, the correct answer is
`( (8, -{2π}{3}) ), ( (-8, {2π}{3}) ), ( (8, {4π}{3}) )`. This can be confirmed by converting these polar coordinates back to Cartesian coordinates and ensuring they represent the same point in the plane.

It's essential to understand the periodic nature of polar coordinates; adding or subtracting a multiple of 2π to the angle results in the same point. In this case, subtracting 2π repeatedly generated the three additional representations.