Question

Solve the inequality

Answer 1

x ≤ -3

Explanation:

We can solve the inequality using the following steps:

• Note that 1 is the same as 1/1.

Step 1: Multiply the entire equation by the least common denominator (LCD):

• The least common denominator (LCD) is the smallest number by which a set of fractions can be divided by.
• Since we have some variables, it will mostly allow us to clear the denominator.
• We treat it like the greatest common factor (GCF) of the denominators.
• Thus, the LCD is given by:

3 * 2 * 1 = 6

Now, we multiply the entire equation by 6 to clear the fractions:

Multiplying x/3 by 6:

`6((x)/(3))\\ \\(6x)/(3)\\ \\2x`

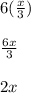
Multiplying - [(x - 1) / 2] by 6:

`6[-((x-1))/(2)]\\ \\-(6x-6)/(2)\\ \\-((6x)/(2)+(-6)/(2))\\ \\ -(3x-3)\\\\-3x+3`

Multiplying 1 by 6:

`6(1)\\6\\`

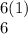
Thus, our inequality with no fractions is given by:

`2x-3x+3\geq 6`

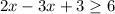
Step 2: Combine like terms on the left-hand side:

`-x+3\geq 6`

Step 3: Subtract 3 from both sides:

`(-x+3\geq 6)-3\\\\-x\geq 3`

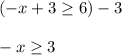
Step 4: Divide both sides and flip the sign to solve the inequality:

`((-x\geq 3))/(-1)\\ \\x\leq -3`

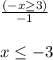
Therefore, x ≤ -3 is the solution to the inequality.