Question

Please help. It’s algebra 2

Answer 1

The polynomial function of least degree with rational coefficients, a leading coefficient of 1, and the given value of 4.6 - √7 is:

`f(x) = x^2 - 7` (in standard form)

How to create a polynomial function

To create a polynomial function of least degree with rational coefficients, a leading coefficient of 1, and the given value of 4.6 - √7, use the concept of conjugate pairs.

The conjugate of √7 is -√7.

The conjugate pairs allow us to eliminate the irrational part (√7) by utilizing the difference of squares. The product of a conjugate pair results in a rational expression.

Let's denote x as the irrational part (√7) and create the polynomial function:

`f(x) = (x - (\sqrt7))(x - (-\sqrt7))`

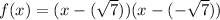
Expanding the expression:

`f(x) = (x - \sqrt7)(x + \sqrt7)\\f(x) = x^2 - \sqrt7x + \sqrt7x - (\sqrt7)(-\sqrt7)\\f(x) = x^2 - (\sqrt7)(-\sqrt7)\\f(x) = x^2 - 7`

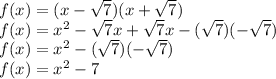
Therefore, the polynomial function of least degree with rational coefficients, a leading coefficient of 1, and the given value of 4.6 - √7 is:

`f(x) = x^2 - 7` (in standard form)