The equation of the line of best fit is y = -0.83x + 2.84
When x = 10, the predicted value of y is approximately -5.46.
How to find the equation of the line of best fit
To find the equation of the line of best fit, we can use linear regression. Let's calculate it using the data you provided:
x: 0, 1, 2, 3, 4, 5, 6, 7
y: 12, 8, 5, 3, 2, 3, 5, 8
We can use the least squares method to find the equation of the line of best fit.
The equation of a line is y = mx + b, where m is the slope and b is the y-intercept.
First, calculate the means of x and y:
Mean of x (
) = (0 + 1 + 2 + 3 + 4 + 5 + 6 + 7) / 8 = 3.5
Mean of y (
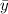) = (12 + 8 + 5 + 3 + 2 + 3 + 5 + 8) / 8 = 5.75
Next, calculate the deviations from the means for both x and y:
Deviation of x (dx) = x -
Deviation of y (dy) = y -
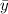
Now, calculate the sum of the products of the deviations for each data point:
Σ(dx * dy) = (0 - 3.5)(12 - 5.75) + (1 - 3.5)(8 - 5.75) + (2 - 3.5)(5 - 5.75) + (3 - 3.5)(3 - 5.75) + (4 - 3.5)(2 - 5.75) + (5 - 3.5)(3 - 5.75) + (6 - 3.5)(5 - 5.75) + (7 - 3.5)(8 - 5.75)
= (-3.5)(6.25) + (-2.5)(2.25) + (-1.5)(-0.75) + (-0.5)(-2.5) + (0.5)(-2.75) + (1.5)(-3.75) + (3.5)(-2.75) + (3.5)(2.25)
= -34.875.
Next, calculate the sum of the squared deviations of x:
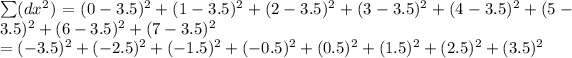
= 42
Now, calculate the slope (m) of the line of best fit:
m = Σ(dx * dy) / Σ(
) = -34.875 / 42 ≈ -0.83
Finally, calculate the y-intercept (b) of the line of best fit:
b =
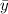- m *
= 5.75 - (-0.83) * 3.5 ≈ 2.84
Therefore, the equation of the line of best fit is:
y = -0.83x + 2.84
To predict y when x = 10, we can substitute x = 10 into the equation:
y = -0.83 * 10 + 2.84
= -5.46
Therefore, when x = 10, the predicted value of y is approximately -5.46.