Question

Collect marks obtained by different students And calculate standard deviation MD from mean and MD from median​

Answer 1

The standard deviation from the mean (MD) is approximately 10.60, and the standard deviation from the median (MD) is approximately 10.65.

How to calculate the standard deviation

To calculate the standard deviation from the mean (MD) and the standard deviation from the median (MD), we can follow these steps:

Calculate the mean of the data set.

Calculate the median of the data set.

Calculate the difference between each data point and the mean (or median).

Square each difference obtained in step 3.

Calculate the average of the squared differences obtained in step 4.

Take the square root of the average obtained in step 5 to get the standard deviation.

Given marks: 17, 35, 38, 16, 42, 27, 19, 11, 40, 25

Step 1: Calculate the mean.

mean = (17 + 35 + 38 + 16 + 42 + 27 + 19 + 11 + 40 + 25) / 10

mean = 270 / 10

mean = 27

Step 2: Calculate the median.

First, arrange the data set in ascending order: 11, 16, 17, 19, 25, 27, 35, 38, 40, 42

Since the data set has an even number of values, the median is the average of the two middle values.

median = (25 + 27) / 2

median = 52 / 2

median = 26

Step 3: Calculate the difference between each data point and the mean (or median).

For the mean:

17 - 27 = -10

35 - 27 = 8

38 - 27 = 11

16 - 27 = -11

42 - 27 = 15

27 - 27 = 0

19 - 27 = -8

11 - 27 = -16

40 - 27 = 13

25 - 27 = -2

For the median:

11 - 26 = -15

16 - 26 = -10

17 - 26 = -9

19 - 26 = -7

25 - 26 = -1

27 - 26 = 1

35 - 26 = 9

38 - 26 = 12

40 - 26 = 14

42 - 26 = 16

Step 4: Square each difference obtained in step 3.

For the mean:

`(-10)^2 = 100\\8^2 = 64\\11^2 = 121\\(-11)^2 = 121\\15^2 = 225\\0^2 = 0\\(-8)^2 = 64\\(-16)^2 = 256\\13^2 = 169\\(-2)^2 = 4`

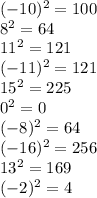
For the median:

`(-15)^2 = 225\\(-10)^2 = 100\\(-9)^2 = 81\\(-7)^2 = 49\\(-1)^2 = 1\\1^2 = 1\\9^2 = 81\\12^2 = 144\\14^2 = 196\\16^2 = 256`

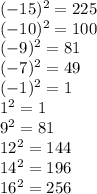
Step 5: Calculate the average of the squared differences obtained in step 4.

For the mean:

(100 + 64 + 121 + 121 + 225 + 0 + 64 + 256 + 169 + 4) / 10

= 1124 / 10

= 112.4

For the median:

(225 + 100 + 81 + 49 + 1 + 1 + 81 + 144 + 196 + 256) / 10

= 1134 / 10

= 113.4

Step 6: Take the square root of the average obtained in step 5 to get the standard deviation.

For the mean:

Standard Deviation (MD from mean) = √(112.4)

≈ 10.60 (rounded to two decimal places)

For the median:

Standard Deviation (MD from median) = √(113.4)

≈ 10.65 (rounded to two decimal places)

Therefore, the standard deviation from the mean (MD) is approximately 10.60, and the standard deviation from the median (MD) is approximately 10.65.

Given below are the marks obtained by different students of a class. calculate standard deviation MD from mean and MD from median​

Marks 17 35 38 16 42 27 19 11 40 25