Given that cylinder A and B are mathematically similar, the volume of cylinder B is 720

How to calculate volume of a cylinder
Since the cylinders A and B are mathematically similar, their corresponding dimensions are proportional.
The ratio of their heights is given as 5:10, which simplifies to 1:2.
We are given that the area of the cross-section of cylinder A is 18
 . Let's denote the radius of cylinder A as
. Let's denote the radius of cylinder A as
 . The formula for the area of the cross-section of a cylinder is A = π
. The formula for the area of the cross-section of a cylinder is A = π
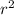 .
.
Given that
 = 18
= 18
 , we can solve for
, we can solve for
 :
:
 = π
= π
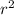
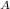
18 = π
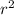
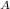
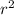
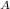 = 18/π
= 18/π
 = √(18/π)
= √(18/π)
Now, find the volume of cylinder B using the corresponding dimensions. Let's denote the radius of cylinder B as
 and its height as
and its height as
 .
.
Since the volume of a cylinder is given by V = π
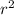 h, and the cylinders A and B are mathematically similar, their volumes are proportional to the cube of their corresponding dimensions.
h, and the cylinders A and B are mathematically similar, their volumes are proportional to the cube of their corresponding dimensions.
The ratio of their volumes is
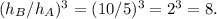
Therefore, the volume of cylinder B is 8 times the volume of cylinder A.
 = 8 *
= 8 *

 = 8 * (π
= 8 * (π
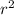
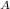
 )
)
 = 8 * (π * (18/π) * 5)
= 8 * (π * (18/π) * 5)
 = 8 * (18 * 5)
= 8 * (18 * 5)
 = 720
= 720

Therefore, the volume of cylinder B is 720

A and B are two cylinders that are mathematically similar. The area of the cross-section of cylinder A is 18cm^2. The height of cylinder A is 5cm while height of cylinder B is 10cm
Work out the volume of cylinder B.