Question

Javier and Ercila are supervisors at a shopping mall. Each was given the task of estimating the mean distance that shoppers live from the mall. They each randomly surveyed 100 shoppers. The samples yielded the following information: Javier: x= 6.0 miles, s= 6.0 miles Ercila: x= 6.0 miles, s= 7.0 miles How can you determine which survey was correct? a. Ercilla's survey was correct because the standard deviation is only 1.0 mile away from the mean distance shoppers live from the mall. b. Javier's survey was correct because the standard deviation is only 2.0 miles away from the mean distance shoppers live from the mall. c. Ercilla's survey was correct because the standard deviation is greater than the mean distance shoppers live from the mall. d. Javier's survey was correct because the standard deviation is less than the mean distance shoppers live from the mall. e. There is no way to determine from these numbers which survey was correct.

Answer 1

The data for the survey are required to calculate the mean and the standard deviation. The correct option is therefore;

e. There is no way to determine from these numbers which survey was correct

What is a survey; A survey is an administered set of questions which are used to extract information with regards to desired topics.

The mean of a data set is the ratio of the sum of the values in the dataset to the count or size of the data

The standard deviation measures the variation of the values from the mean. The standard deviation is the square root of the variance. The variance is mean of the sum of the square of the deviation from the mean

The formula for the standard deviation is;
`\sigma =\sqrt{(\sum(x_i-\mu)^2)/(N) }`

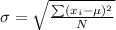
The above equation indicates that the standard deviation depend on the mean, μ, and the sample size, N,

The formula for the standard deviation of a sample is;
`s=\sqrt{\frac{\sum(x_i-\bar{x})^2}{N-1} }`

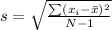
Where;
`\bar{x}` is the mean and s is the standard deviation

The details for the survey are;

Sample size, N = 100

Javier,
`\bar{x}` = 6.0, s = 6.0

Ercila,
`\bar{x}` = 6.0, s = 7.0

The data for the survey and above equation for the standard deviation indicates that more information is required to determine the correct values for the mean and standard deviation

The correct option is therefore;

e. There is no way to determine from these numbers which survey was correct