Answer:
See below
Explanation:
Let's go through each expression one by one:
1.




2.




3.



Since
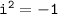 , replace
, replace
 with
with
 :
:


4.



Since
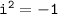 , replace
, replace
 with
with
 :
:


5.



Since
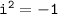 , replace
, replace
 with
with
 :
:


6.

First, multiply the first two terms:



Replace
 with
with
 :
:

Now, distribute:

Replace
 with
with
 :
:

7.


Use FOIL:

Replace
 with
with
 :
:


8.

Use the difference of squares formula:




Replace
 with
with
 :
:


9.

Multiply the numerator and denominator by
 to eliminate the denominator:
to eliminate the denominator:

Replace
 with
with
 :
:


10.

Multiply the numerator and denominator by
 to eliminate the denominator:
to eliminate the denominator:


Replace
 with
with
 :
:

