Question

How many solutions does this system of equations have? Explain how you know.

(y = -2x - 3
(8x + 4y = 20

Answer 1

Let's solve the 2nd equation for y to get it into y = mx+b form.

8x + 4y = 20

4y = -8x + 20

y = (-8x + 20)/4

y = (-8x)/4 + 20/4

y = -2x + 5

The original system

`\begin{cases}\text{y} = -2\text{x} - 3\\8\text{x} + 4\text{y} = 20\end{cases}`

is the same as this system

`\begin{cases}\text{y} = -2\text{x} - 3\\\text{y} = -2\text{x} + 5\end{cases}`

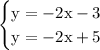
Both have the same slope (-2) but different y intercepts. This will mean the two lines are parallel. Parallel lines never intersect.

There are no solutions. The system is inconsistent

--------------------------

Here's another approach

8x + 4y = 20

8x + 4(-2x-3) = 20 ... replace y with -2x-3

8x - 8x - 12 = 20

0x - 12 = 20

0 - 12 = 20

-12 = 20 ... false

The last equation is false, so the first equation is false when y = -2x-3

This is another way to see that the system is inconsistent that has no solutions.