Question

Which are correct representations of the inequality –3(2x – 5) < 5(2 – x)? Select two options.

x < 5
–6x – 5 < 10 – x
–6x + 15 < 10 – 5x
A number line from negative 3 to 3 in increments of 1. An open circle is at 5 and a bold line starts at 5 and is pointing to the right.
A number line from negative 3 to 3 in increments of 1. An open circle is at negative 5 and a bold line starts at negative 5 and is pointing to the left.

Answer 1

`\\ \rm\leadsto -3(2x-5)<5(2-x)`

• a(b+c)=ab+ac

`\\ \rm\leadsto -6x+15<10-5x`

Option C

`\\ \rm\leadsto -x<-5`

`\\ \rm\leadsto x>5`

Rest are wrong

Answer 2

–6x + 15 < 10 – 5x

A number line from negative 3 to 7 in increments of 1. An open circle is at 5 and a bold line starts at 5 and is pointing to the right.

Explanation:

Given inequality

`-3(2x-5) < 5(2-x)`

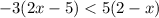
Solving the inequality

Expand the brackets:

`\implies -6x+15 < 10-5x`

Add 6x to both sides:

`\implies 15 < 10+x`

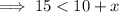
Subtract 10 from both sides:

`\implies 5 < x`

`\implies x > 5`

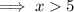
Therefore, x is bigger than 5.

Graphing the inequality

When graphing inequalities on a number line:

• < or > = open circle
• ≤ or ≥ = closed circle
• < or ≤ = shade to the left
• > or ≥ = shade to the right

To graph the given inequality on a number line:

• place an open circle at 5
• draw a line starting at 5 and pointing to the right

Conclusion

Therefore, the correct representations of the given inequality are:

• –6x + 15 < 10 – 5x
• A number line from negative 3 to 7 in increments of 1. An open circle is at 5 and a bold line starts at 5 and is pointing to the right.