Question

MATH 100 POINTS

a square with sides of lentgh x is inside a circle. each vertex of the square is on the circumference of the circle. the area of the cirlce is 64cm^2 work out the value of x to 3sf

Answer 1

The side length of the square x is 6.38

How to find x

To find the value of x, we can use the fact that the square is inscribed in the circle, meaning that the diagonal of the square is equal to the diameter of the circle.

Let D be the diameter of the circle, and x be the side length of the square.

The diagonal of the square is

D = x√2

The area of the circle is given by A = πr² = π (D/2)²

64 = π (x√2 / 2)²

64 = π (x² * 2 / 4)

64 = π (x²/2)

128 = π x²

x² = 128 / π

x = √(128 / π)

x = 6.38

Therefore, the value of x to three significant figures is x = 6.38 cm

Answer 2

x = 383

Explanation:

Let's denote the side length of the square as
`\sf x` and the radius of the circle as
`\sf r`.

Since the vertices of the square lie on the circumference of the circle, the diagonal of the square is also the diameter of the circle.

The diagonal of the square can be found using the Pythagorean theorem. If
`\sf s` is the side length of the square, then the diagonal
`\sf d` is given by:

`\sf d = √(s^2 + s^2) = √(2s^2) = s√(2)`

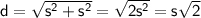
Since the diagonal is also the diameter of the circle,
`\sf d = 2r`.

Therefore:

`\sf x√(2) = 2r`

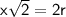
Now, we know that the area (
`\sf A`) of the circle is given by
`\sf \pi r^2` and it is given that
`\sf A = 64 \, \text{cm}^2`.

Substitute
`\sf r = (x√(2))/(2)` into the area formula:

`\sf \pi \left( (x√(2))/(2) \right)^2 = 64`

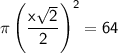
Now, solve for
`\sf x`:

`\sf (\pi x^2)/(2) = 64`

`\sf \pi x^2 = 128`

`\sf x^2 = (128)/(\pi)`

`\sf x = \sqrt{(128)/(\pi)}`

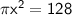
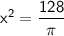
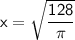
Now, calculate the numerical value:

`\sf x \approx 6.383076486 \, \text{cm}`

`\sf x \approx 6.383 \, \text{cm (in 3 s.f.)}`

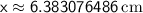
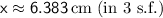
Therefore, the value of
`\sf x` (to 3 significant figures) is approximately
`\sf 6.383 \, \text{cm}`.