Question

Use Pascal's Triangle to help find the missing values. x^4-4x^b+6x^2-ax+1

a=

b=​

Answer 1

The value of a = 4 , b = 3

Explanation:

Given the equation,

x⁴ - 4
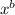`x^(b)` + 6x² - ax + 1

so, the coefficients are - 1 4 6 a 1

the Pascal's triangle is as follows :

1

1 2

1 2 1

1 3 3 1

1 4 6 4 1

So,

from Pascal's triangle ,

we can see that , after comparing with given equation , we get

Row n = 4

The coefficient be 1 4 6 4 1

∴ we get

a = 4

and

(x+y)⁴ = x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴

Now, as given equation be x⁴ - 4
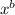`x^(b)` + 6x² - ax + 1

By comparing we get y = -1 and b = 3

So, we get

a = 4 , b = 3