Question

Given events J and K: P(J) = 0.18; P(K) = 0.37; P(J OR K) = 0.45. Create a Venn Diagram of these events.

Answer 1

The probability of both J and K occurring (their intersection) is 0.10.

How to find events?

To find the intersection of events J and K:

Given the probabilities:

`\( P(J) = 0.18 \)`

`\( P(K) = 0.37 \)`

`\( P(J \text{ OR } K) = 0.45 \)`

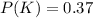
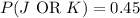
Use the formula for the probability of the union of two events:

`\[ P(J \text{ OR } K) = P(J) + P(K) - P(J \text{ AND } K) \]`

To find
`\( P(J \text{ AND } K) \)`, rearrange this equation:

`\[ P(J \text{ AND } K) = P(J) + P(K) - P(J \text{ OR } K) \]`

Substituting in the given values:

`\[ P(J \text{ AND } K) = 0.18 + 0.37 - 0.45 \]`

`\[ P(J \text{ AND } K) = 0.55 - 0.45 \]`

`\[ P(J \text{ AND } K) = 0.10 \]`

So, the probability of both J and K occurring (their intersection) is 0.10. This was represented in the overlapping area of the Venn Diagram.