Question

Q3. In how many years will *4000 grow to 4140 at rate of 5% compounded quarterly?​

Answer 1

Exact answer: 0.2507341099 years

Rounded answer (nearest hundredth): 0.25 years

Explanation:

The compound interest formula:

The formula for compound interest is given by:

`A(t)=P(1+r/n)^(^n^t^)`, where:

• A(t) is the amount in the account after t years,
• P is the principal (aka the deposit),
• r is the interest rate (the percentage is converted to a decimal)
• and n is the number of compounding periods.

Identifying which values to substitute for the variables and solving for t:

• A = 4140, since the amount in the account after t years is $4140.
• P = 4000 since the $4000 is the principal.
• r = 0.05, since 5% as a decimal is 0.05.
• n = 4, since a quarter is 4.

Now, we can solve for t using the following steps:

Step 1: Plug in 4140 for A, 4000 for P, 0.05 for r, and n for 4. Then, simplify as much as possible:

`4140 = 4000(1+0.05/4)^(^4^t^)\\\\4140=4000(1.0125)^(^4^t^)`

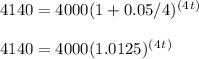
Step 2: Distribute 4000:

`4140=(4000*1.0125)^(^4^t^)\\\\4140=4050^4^t`

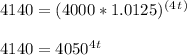
Step 3: Take the log of both sides. Then, apply the power rule of logs to bring 4t down to the front:

`log(4140)=log(4050^4^t)\\\\log(4140)=4t*log(4050)`

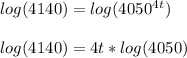
Step 4: Divide both sides by log(4050):

`(log(4140)=4t*log(4050))/(log(4050)) \\\\(log(4140))/(log(4050)) =4t`

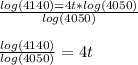
Step 5: Multiply both sides by 1/4 to solve for t:

`((log(4140))/(log(4050)) =4t)*(1)/(4)\\\\\\0.2507341099=t\\\\0.25=t`

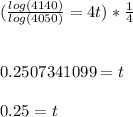
Therefore it will take about 0.25 years for the $4000 deposit to grow to 4140.

• You can put the exact answer or use the rounded answer, depending on whichever you're used to using in your particular class.