Question

The drama club is selling tickets to their play to raise money for the show's expenses. Each student ticket sells for $4 and each adult ticket sells for $8. The auditorium can hold at most 130 people. The drama club must make a minimum of $750 from ticket sales to cover the show's costs. Also, they can sell no more than 30 student tickets and no more than 100 adult tickets. If xx represents the number of student tickets sold and yy represents the number of adult tickets sold, write and solve a system of inequalities graphically and determine one possible solution.

Answer 1

One possible feasible solution is ( 30, 79 )

Explanation:

Let's set up the inequalities based on the given conditions:

The total number of tickets sold should be at most 130:

x (number of student tickets) + y (number of adult tickets) ≤ 130

The total revenue from ticket sales must be at least $750:

4x (revenue from student tickets) + 8y (revenue from adult tickets) ≥ 750

The number of student tickets sold (x) should be no more than 30:

x ≤ 30

The number of adult tickets sold (y) should be no more than 100:

y ≤ 100

The objective of this problem is to maximize ticket sales

Max
`4x+8y\geq 750`

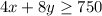
You can use the Demos Graphing calculator website to plot these graphs where you find these corner points.

Points 4x+8y>= 750

(0,0) 0

(30,0) 120

(30, 79) 752

so x= 30 and y =79
We sell 30 tickets to the students and 79 tickets to the adults and its satisfy our all the conditions