Let's consider triangle ABC
Length AB can be obtained using Pythagoras
![\begin{gathered} AB^2=x^2+y^2 \\ AB\text{ = }\sqrt[]{x^2+y^2} \\ \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/s80paky0rn8mxeczcqdy.png)
Similarly, we can consider triangle ACD, so that length AD will be obtained through Pythagoras
![\begin{gathered} AD^2=x^2+z^2 \\ AD\text{ = }\sqrt[]{x^2+z^2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/sujh4oujwyk62n9a52hy.png)
Considering triangle ABD, with BD being the hypotenuse
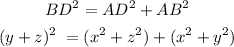
Expanding the parentheses
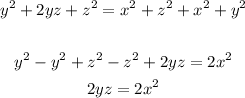
Divide both sides by 2
![\begin{gathered} (2yz)/(2)=\text{ }(2x^2)/(2) \\ yz=x^2 \\ \\ x^2\text{ =yz} \\ \\ x\text{ = }\sqrt[]{yz} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/swk46abivxryrawniabn.png)
Option A is correct