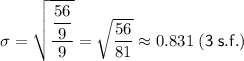Question

Please Answer this question ASAP.

Answer 1

`\textsf{A. Mode $=\boxed{7}$}`

`\textsf{B. Median $=\boxed{7}$}`

`\textsf{C. Mean $=\boxed{(68)/(9) \approx 7.56}$}`

`\textsf{D. $\sf Q_1 =\boxed{7}$}`

`\textsf{E. $\sf Q_3 =\boxed{8.5}$}`

`\textsf{F. $\sf IQR =\boxed{1.5}$}`

`\textsf{G. Sample\;standard\;deviation\;$=\boxed{0.882}$}`

`\textsf{G. Population\;standard\;deviation\;$=\boxed{0.831}$}`

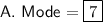
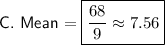
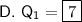
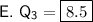
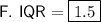
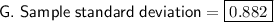
Explanation:

The given data set in ascending order is:

• 7, 7, 7, 7, 7, 7, 8, 9, 9

`\hrulefill`

Mode

The mode of a data set is the value or values that occur most frequently. Therefore, the mode of the given data set is:

`\large\textsf{Mode $=\boxed{7}$}`

`\hrulefill`

Median

The median of a data set is the middle value when the values are arranged in ascending or descending order. Since the given data set has a total of 9 values, the median is the 5th value:

`\large\textsf{Median $=\boxed{7}$}`

`\hrulefill`

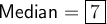
Mean

The mean (average) of a data set is calculated by summing all the values in the data set and then dividing the total by the number of data values. Therefore, the mean of the given data set is:

`\large\textsf{Mean $=(7 + 7 + 7 + 7 + 7 + 7 + 8 + 9 + 9)/(9)=\boxed{(68)/(9)}$}`

`\hrulefill`

Lower Quartile (Q1)

The lower quartile (Q1) of a data set is the median of the lower half of the dataset. As there are 4 data values to the left of the median, the lower quartile is the average of the middle two data values:

`\large\textsf{$Q_1=(7+7)/(2)=\boxed{7}$}`

`\hrulefill`

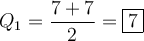
Upper Quartile (Q1)

The upper quartile (Q3) of a data set is the median of the upper half of the dataset. As there are 4 data values to the right of the median, the upper quartile is the average of the middle two data values:

`\large\textsf{$Q_3=(8+9)/(2)=\boxed{8.5}$}`

`\hrulefill`

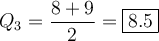
Interquartile Range (IQR)

The interquartile range (IQR) of a data set is the difference between the third quartile (Q3) and the first quartile (Q1):

`\large\textsf{$IQR=8.5-7=\boxed{1.5}$}`

`\hrulefill`

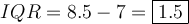
Standard Deviations

To calculate both the sample standard deviation and the population standard deviation, we must first calculate the sum of the square of each data value less the mean.

As there are only 3 different data values, we can calculate the square of each data value less the mean as follows:

`\left(7-(68)/(9)\right)^2=(25)/(81)`

`\left(8-(68)/(9)\right)^2=(16)/(81)`

`\left(9-(68)/(9)\right)^2=(169)/(81)`

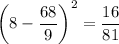
There are six 7s, one 8 and two 9s in the data set, so the sum of the square of each data value less the mean is:

`\displaystyle \sum \left(\sf data \;value - mean\right)^2=6 \cdot (25)/(81)+(16)/(81)+2 \cdot (169)/(81)=(56)/(9)`

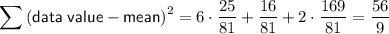
The formula for the sample standard deviation is:

`S=\sqrt{\frac{\displaystyle \sum \left(x_i-\overline{x}\right)^2}{n-1}}`

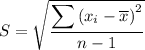
where
`\overline{x}` is the mean, and n is the number of data values.

Therefore, the sample standard deviation of the given data set is:

`S=\sqrt{((56)/(9))/(9-1)}=\sqrt{(7)/(9)}=(√(7))/(3)\approx0.882\; \sf (3\;s.f.)`

`\large\textsf{Sample\;standard\;deviation\;$=\boxed{0.882}$}`

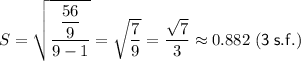
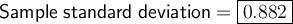
The formula for the population standard deviation is:

`\sigma=\sqrt{(\displaystyle \sum \left(x_i-\mu\right)^2)/(n)}`

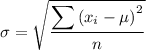
where μ is the mean, and n is the number of data values.

Therefore, the population standard deviation of the given data set is:

`\sigma=\sqrt{((56)/(9))/(9)}=\sqrt{(56)/(81)}\approx 0.831\; \sf (3\;s.f.)`

`\large\textsf{Population\;standard\;deviation\;$=\boxed{0.831}$}`