Question

A cannon launches a ball at 97.8m/s at an angle of 43.4 how long did it take to hit the ground

Answer 1

`$13.714$` seconds

Problem Solving Strategy:

• What we have here is a projectile motion problem. The equation for the y-component of an object's velocity in projectile motion is
  `$v_y=v_(0y)-gt`. Here,
  `v_y` is the y-component of the object's velocity.
  `v_(0y)` is the y-component of the objects initial velocity, and
  `g` is the gravitational constant
  `$9.8$`
  `m/s^2`.
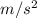• I've additionally attached a useful figure below to help visualize the concepts presented.

Step 1: Find the y-component of the cannon ball's initial velocity,
`v_(0y)`.

• 
  `v_(0y)=v_0\sin(\theta) = 97.8\sin(43.4)\approx67.197\:$ m/s`

Step 2: At the peak of the projectile motion, the y-component of the ball's velocity,
`v_y` will be equal to zero. Using this fact, we can solve for the time it takes to reach the peak of the parabola, which will be useful in the following steps.

• 
  `$v_y=v_(0y)-gt`
• 
  `$\Rightarrow 0=67.197-(9.8)t$`
• 
  `$\Rightarrow t=6.857` seconds

Step 3: Since the object has reached its maximum height in 6.857 seconds, we can conclude the total time is equal to
`2*6.857=13.714` seconds. We can see from the figure that the maximum height is reached at half of the final time. So doubling this will give us our final time.