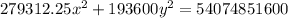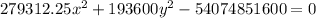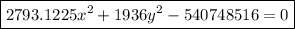Question

URGENT please help solve these questions and graph

Answer 1

`\textsf{1)}\quad \textsf{Center:}\quad (0, 0)`

`\begin{aligned}\textsf{2)}\quad &\textsf{Minor vertices:}\quad (-440, 0)\;\textsf{and}\;(440, 0)\\ &\textsf{Major vertices:}\quad (-528.5, 0)\;\textsf{and}\; (528.5, 0)\end{aligned}`

`\textsf{3)}\quad \textsf{Foci:}\quad (0, -292.8)\;\textsf{and}\;(0, 292.8)`

`\begin{aligned}\textsf{4)}\quad &\textsf{General form:} \quad (x^2)/(193600)+(y^2)/(279312.25)=1\\\\ &\textsf{Standard form:}\quad 2793.1225x^2+1936y^2-540748516=0\end{algned}`

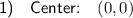
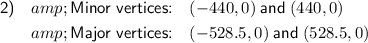
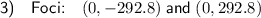
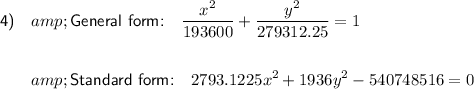
Explanation:

The provided ellipse is a vertical ellipse.

The general equation of a vertical ellipse is:

`\boxed{\begin{array}{l}\underline{\textsf{General equation of a vertical ellipse}}\\\\((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1\\\\\textsf{where:}\\\phantom{ww}\bullet\textsf{$2b=$ major axis}\\\phantom{ww}\bullet\textsf{$2a=$ minor axis}\\\phantom{ww}\bullet \textsf{$(h,k)=$ center}\\\phantom{ww}\bullet\textsf{$(h,k\pm b)=$ major vertices}\\\phantom{ww}\bullet\textsf{$(h\pm a,k)=$ minor vertices}\\\phantom{ww}\bullet\textsf{$(h,k\pm c)=$ foci where $c^2=b^2-a^2$}\end{array}}`

Let the center of the ellipse be the origin (0, 0), so:

`h = 0`

`k = 0`

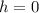
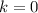
The major axis of an ellipse is the longest diameter. Therefore, the major axis is 1057, so:

`2b=1057 \implies b=(1057)/(2)=528.5`

The minor axis of an ellipse is the shortest diameter, perpendicular to the major axis. Therefore, the minor axis is 880, so:

`2a=880 \implies a=(880)/(2)=440`

The formula for the minor vertices is (h±a, k), so:

`\begin{aligned}\sf Minor\;vertices&=(h\pm a, k)\\&=(0 \pm 440, 0)\\&=(\pm 440,0)\end{aligned}`

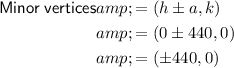
The formula for the major vertices is (h, k±b), so:

`\begin{aligned}\sf Major\;vertices&=(h,k\pm b)\\&=(0, 0\pm 528.5)\\&=(0,\pm 528.5)\end{aligned}`

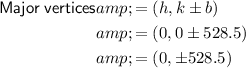
To determine the coordinates of the foci, first calculate the value of c:

`\begin{aligned}c^2&=b^2-a^2\\c^2&=(528.5)^2-(440)^2\\c&=√((528.5)^2-(440)^2)\\c&=√(85712.25)\end{aligned}`

Now, substitute the values of h, k and c into the formula for the foci:

`\begin{aligned}\sf Foci&=(h, k\pm c)\\&=(0,0\pm √(85712.25))\\&=(0,\pm 292.8)\end{aligned}`

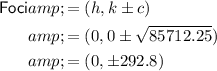
To find the equation of the ellipse, substitute the values of a, b, h and k into the formula:

`((x-0)^2)/((440)^2)+((y-0)^2)/((528.5)^2)=1`

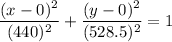
Simplify:

`\boxed{(x^2)/(193600)+(y^2)/(279312.25)=1}`

To write this in standard form:

`x^2+(193600y^2)/(279312.25)=193600`

`279312.25x^2+193600y^2=54074851600`

`279312.25x^2+193600y^2-54074851600=0`

`\boxed{2793.1225x^2+1936y^2-540748516=0}`