Question

URGENT PLEASE ANSWER

Answer 1

`\boxed{\sf y = (3)/(2)x + (7)/(2)}`

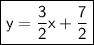
Explanation:

To find the equation of the line that passes through the points (1, 5), (3, 8), (5, 11), and (7, 14), we can use the slope-intercept form of a linear equation:
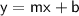`\sf y = mx + b`, where
`\sf m` is the slope and
`\sf b` is the y-intercept.

First, find the slope (
`\sf m`) using two of the given points.

Let's use the first two points (1, 5) and (3, 8):

`\sf m = (y_2 - y_1)/(x_2 - x_1)`

`\sf m = (8 - 5)/(3 - 1)`

`\sf m = (3)/(2)`

Now that we have the slope, let's use one of the points to find the y-intercept (
`\sf b`).

Let's use the point (1, 5):

`\sf 5 = (3)/(2) \cdot 1 + b`

`\sf 5 = (3)/(2) + b`

`\sf b = (7)/(2)`

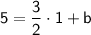
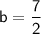
Now, we have the slope
`\sf \left( m = (3)/(2)\right)` and the y-intercept
`\left(\sf b = (7)/(2) \right)`.

Substitute these values into the slope-intercept form:

`\sf y = (3)/(2)x + (7)/(2)`

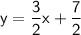
So, the equation of the line that passes through the given points is:

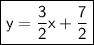`\boxed{\sf y = (3)/(2)x + (7)/(2)}`.