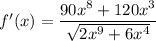Question

Shown below is the image for my question. If you are knowledgeable in calculus you may know how to answer it. It has to do with derivatives and chain rule.

I really appreciate your time and help!!

Answer 1

The chain rule says:

\[\dfrac{d}{dx}\left[f\Bigl(g(x)\Bigr)\right]=f'\Bigl(g(x)\Bigr)g'(x)\]

It tells us how to differentiate composite functions.

Explanation:

Answer 2

`f'(x)=(90x^8+120x^3)/(√(2x^9+6x^4))`

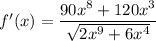
Explanation:

Given function:

`f(x)=10√(2x^9+6x^4)`

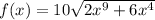
The chain rule helps differentiate complicated functions by splitting them up into functions that are easier to differentiate.

Once we've worked out how to split up the function, we can differentiate it using the chain rule formula:

`\boxed{\begin{array}{c}\underline{\text{Chain Rule for Differentiation}}\\\\\text{If\;\;$y=f(u)$\;\;and\;\;$u=g(x)$\;\;then:}\\\\\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}*\frac{\text{d}u}{\text{d}x}\end{array}}`

`\textsf{Let}\;\;y=10√(u)\;\;\textsf{where}\;\;u=2x^9+6x^4`

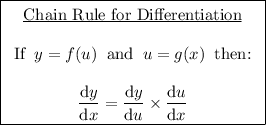
Differentiate the two parts separately:

`\begin{aligned}y=10u^(\frac12)\implies \frac{\text{d}y}{\text{d}u}&=(1)/(2) \cdot 10u^(\frac12-1)\\\\ \frac{\text{d}y}{\text{d}u}&=5u^(-\frac12)\\\\\frac{\text{d}y}{\text{d}u}&=(5)/(√(u))\end{aligned}`

`\begin{aligned}u=2x^9+6x^4\implies \frac{\text{d}u}{\text{d}x}&=9\cdot 2x^(9-1)+4 \cdot 6x^(4-1)\\\\\frac{\text{d}u}{\text{d}x}&=18x^8+24x^3\end{aligned}`

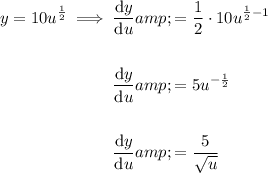
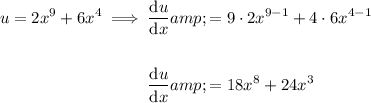
Now, put everything back into the chain rule formula:

`\frac{\text{d}y}{\text{d}x}=(5)/(√(u))* 18x^8+24x^3`

`\frac{\text{d}y}{\text{d}x}=(5( 18x^8+24x^3))/(√(u))`

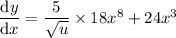
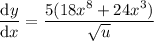
Substitute back in u = 2x⁹ + 6x⁴:

`\frac{\text{d}y}{\text{d}x}=(5(18x^8+24x^3))/(√(2x^9+6x^4))`

`\frac{\text{d}y}{\text{d}x}=(90x^8+120x^3)/(√(2x^9+6x^4))`

Therefore, the derivative of f(x) is:

`f'(x)=(90x^8+120x^3)/(√(2x^9+6x^4))`