Question

A cylinder of gas has a frictionless, massless, tightly sealed piston that is free to move.

The gas temperature is increased from an initial 227°C to a final 327°C. What is the final-to-initial volume ratio Vf /Vi?
A) 1.50
B) 1.33
C) 1.25
D) 1.20
E) 1.00

Answer 1

P V = N R T Ideal gas equation

P1 V1 / T1 = P2 V2 / T2

If P1 = P2 then V1 / T1 = V2 / T2

Or V2 / V1 = T2 / T1 = (327 + 273) / (227 + 273)

V2 / V 1 = 1.20

(D) is correct

Answer 2

D) 1.20

Step-by-step explanation:

To find the final-to-initial volume ratio
`\sf \left( (V_f)/(V_i)\right)` for an ideal gas undergoing an isochoric (constant volume) process, we can use Charles's Law.

Charles's Law states that, at constant pressure, the volume of a given mass of gas is directly proportional to its absolute temperature.

The ratio of final to initial volume can be expressed as:

`\sf (V_f)/(V_i) = (T_f)/(T_i)`

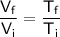
where:

• 
  `\sf V_f` is the final volume,
• 
  `\sf V_i` is the initial volume,
• 
  `\sf T_f` is the final absolute temperature,
• 
  `\sf T_i` is the initial absolute temperature.

Note: Temperatures must be in the absolute scale (Kelvin) for this equation.

Given that the initial temperature is
`\sf 227^\circ C` and the final temperature is
`\sf 327^\circ C`, we need to convert these temperatures to Kelvin:

`\sf T_i = 227 + 273.15`

`\sf T_f = 327 + 273.15`

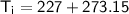
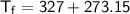
Now, substitute these values into the ratio equation:

`\sf (V_f)/(V_i) = (T_f)/(T_i)`

`\sf (V_f)/(V_i) = (327 + 273.15)/(227 + 273.15)`

`\sf (V_f)/(V_i) \approx (600.15)/(500.15)`

`\sf (V_f)/(V_i) \approx 1.1998`

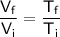
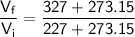
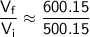
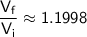
Now, round the result to a reasonable number of significant figures:

`\sf (V_f)/(V_i) \approx 1.20`

Therefore, the correct answer is option (D) 1.20.