Question

The sum of the catheters in a triangle is 27 cm. The corresponding catheter in another right-angled triangle, uniform with the first one, is 2cm and 7cm. Calculate the area of the first triangle.

Answer 1

Given: The sum of the catheters in a triangle is 27 cm

To Determine: The area of the triangle

Solution

Please note the below

Let the first cathetus be x, then the second cathetus would be

`\begin{gathered} c_1=x \\ c_2=27-x \end{gathered}`

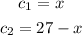
For the second right triangle

`\begin{gathered} c_1=2 \\ c_2=7 \end{gathered}`

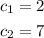
Since the two right triangles are corresponding to each other, then the ratio of their cathethers are equal

Therefore

`\begin{gathered} (x)/(27-x)=(2)/(7) \\ 7x=2(27-x) \\ 7x=54-2x \\ 7x+2x=54 \\ 9x=54 \\ x=(54)/(9) \\ x=6 \end{gathered}`

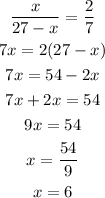
So, the cathethers for the first right triangle would be

`\begin{gathered} c_1=x:c_2=27-x \\ c_1=6 \\ c_2=27-6 \\ c_2=21 \end{gathered}`

Note that the catheters formed the base and the height of the first triangle. The area of a triangle can be calculated using the formula below

`\begin{gathered} Area(triangle)=(1)/(2)* base* height \\ Area(triangle)=(1)/(2)*6cm*21cm \\ Area(triangle)=3cm*21cm \\ Area(triangle)=63cm^2 \end{gathered}`

Hence, the area of the first triangle is 63cm²