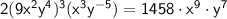Question

YOU MUST SHOW ALL WORK TO RECEIVE FULL CREDIT

Answer 1

3.
`\sf (x^3 \cdot x^(-4))^3 = x^(-3) = (1)/(x^3)`

4.
`\sf 2(9x^2y^4 )^3 (x^3y^(-5)) = 1458 \cdot x^9 \cdot y^7`

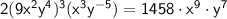
Explanation:

Let's simplify each expression step by step:

3.)
`\sf (x^3 \cdot x^(-4))^3`

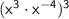
Apply the power rule for exponents, which states that
`\sf (a^m \cdot a^n)^k = a^(m \cdot k + n \cdot k)`:

`\sf (x^3 \cdot x^(-4))^3 = x^((3 \cdot 3 + (-4) \cdot 3))`

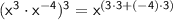
Simplify the exponent:

`\sf = x^((9 - 12)) = x^(-3)`

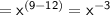
The expression
`\sf x^(-3)` can also be expressed as
`\sf (1)/(x^3)`.

4.)
`\sf 2(9x^2y^4 )^3 (x^3y^(-5))`

Apply the power rule again, distributing the exponents to both the base and the exponent outside the parentheses:

`\sf 2(9x^2y^4 )^3 (x^3y^(-5)) = 2 \cdot 9^3 \cdot (x^2)^3 \cdot (y^4)^3 \cdot x^3 \cdot y^(-5)`

Simplify the coefficients and exponents:

`\sf = 2 \cdot 729 \cdot x^6 \cdot y^(12) \cdot x^3 \cdot y^(-5)`

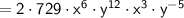
Combine the x-terms by adding their exponents:

`\sf = 1458 \cdot x^9 \cdot y^(12) \cdot y^(-5)`

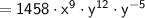
Combine the y-terms by subtracting their exponents:

`\sf = 1458 \cdot x^9 \cdot y^(12-5)`

`\sf = 1458 \cdot x^9 \cdot y^7`

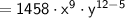
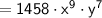
So, the simplified expressions are:

3.
`\sf (x^3 \cdot x^(-4))^3 = x^(-3) = (1)/(x^3)`

4.
`\sf 2(9x^2y^4 )^3 (x^3y^(-5)) = 1458 \cdot x^9 \cdot y^7`