Answer:
0.031 radians/second
Explanation:
A balloon is at a point on the ground 50 m from an observer. If θ is the angle of elevation from the observer to the balloon, and y is the height of the balloon above the ground, the equation that relates θ to y can be found by using the tangent ratio:
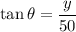
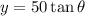
To find the rate of change of the angle of elevation (θ) from the observer to the balloon when the balloon is y meters above the ground, we need to find dθ/dt. To do this, we can use the chain rule:
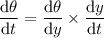
To find dθ/dy, differentiate y = 50 tan θ:
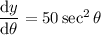
Use the identity sec²θ = 1 + tan²θ:
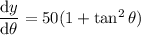
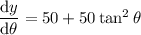
Therefore:

Given the balloon is rising at a rate of 2 m/s:
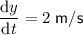
Therefore:
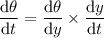
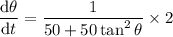
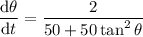
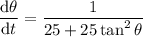
To find the rate of change of the angle of elevation (θ) from the observer to the balloon when the balloon is 27 m above the ground, first find the value of tan θ when y = 27 by substituting y = 27 into y = 50 tan θ:
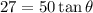
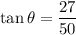
Now, substitute the value of tan θ into dθ/dt:
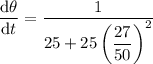
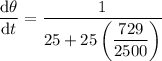
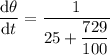
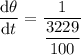
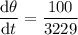
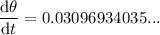

Therefore, the rate of change of the angle of elevation from the observer to the balloon when the balloon is 27 meters above the ground is 0.031 radians/second (rounded to three decimal places).