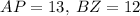Question

B

X
Then AP =
A
BZ =
5
P
Z
-13
12
Given that PX, PY and PZ are perpendicular bisectors of AB, AC and BC
respectively.
If PZ = 5, CZ = 12 and PC = 13.
C

Answer 1

`$AP=13$` and
`$BZ=12$`

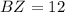
Explanation:

Step 1. We know
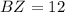`$BZ=12$` because it is congruent to the line segment
`$\overline{CZ}$` as seen in the figure.

Step 2. Consider the Perpendicular Bisector Theorem, which states that any point on the perpendicular bisector is equidistant from both endpoints of the line segment on which it is drawn.

• The 2 endpoints of the line which perpendicular bisector
  `$\overline{PY}$` is drawn are A and C because segments
  `$\overline{AY}` and
  `\overline{YC}` are congruent as shown in the figure.
• Thus, we can conclude that
  `$AP=PC=13$`

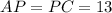
Solution:

`$AP=13,\: BZ=12$`