Question

7) Matt and Ming are selling bottles of water and sports drinks at a school event. A bottle of water sells for $2 and a sports drink sells for $4. At the end of the day they sold 42 items and had total sales of $ 120. If x represents the total number of water bottles sold and y represents the total number of sports drinks sold, how many of each did they sold. ?​

Answer 1

24 water bottles

18 sports drinks

Explanation:

Let's set up a system of equations based on the given information.

Let
`\sf x` be the number of water bottles sold and
`\sf y` be the number of sports drinks sold.

The total number of items sold is given as 42:

`\sf x + y = 42`

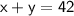
The total sales from water bottles and sports drinks is $120:

`\sf 2x + 4y = 120`

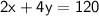
Now, we can solve this system of equations to find the values of
`\sf x` and
`\sf y`.

Let's use the first equation to express
`\sf x` in terms of
`\sf y`:

`\sf x = 42 - y`

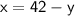
Now, substitute this expression for
`\sf x` into the second equation:

`\sf 2(42 - y) + 4y = 120`

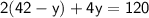
Distribute the 2 on the left side:

`\sf 84 - 2y + 4y = 120`

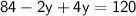
Combine like terms:

`\sf 2y = 36`

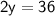
Divide by 2:

`\sf ( 2y )/(2)= (36)/(2)`

`\sf y = 18`

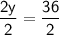
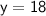
Now that we have the value for
`\sf y`, substitute it back into the expression you found for
`\sf x`:

`\sf x = 42 - 18 = 24`

So, Matt and Ming sold 24 water bottles (
`\sf x`) and 18 sports drinks (
`\sf y`).