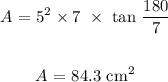Question

Find the area of a regular heptagon with an apothem of 5 cm. Round to the nearest tenth.

Answer 1

`84.3\text{ cm}^2`

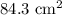
Step-by-step explanation:

Here, we want to calculate the area of the regular heptagon

Mathematically, we use the formula below:

`A\text{ = a}^2n\text{ tan\lparen}(180)/(n))`

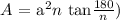
where:

a is the length of the apothem which is 5 cm

n is the number of sides of the polygon which is 7 (heptagon is a 7-sides polygon)

Substituting the values, we have it that:

`\begin{gathered} A\text{ = 5}^2*7\text{ }*\text{ tan }(180)/(7) \\ \\ A\text{ = 84.3 cm}^2 \end{gathered}`