Answer:
10)
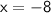
11)
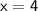
Explanation:
10)
Co-interior angles are angles that are located on the same side of a transversal and between two parallel lines. Co-interior angles are supplementary, which means that they add up to 180 degrees.
In the given case,
 and
and
 are co-interior angles. This means that their measures add up to 180 degrees.
are co-interior angles. This means that their measures add up to 180 degrees.
Therefore, we can write the equation:
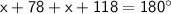
Combining like terms, we get:
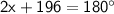
Subtracting 196 from both sides of the equation, we get:
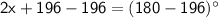
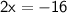
Dividing both sides of the equation by 2, we get:
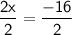
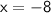
Therefore, the measures of x is -8.
11)
Alternate angles are angles that are located on the opposite sides of a transversal and between two parallel lines. Alternate angles are congruent, which means that they have the same measure.
In the given case,
 and
and
 are alternate angles.
are alternate angles.
This means that their measures are equal.
Therefore, we can write the equation:
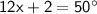
Subtracting 2 from both sides of the equation, we get:
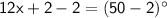
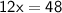
Dividing both sides of the equation by 12, we get:
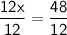
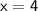
Therefore, the measure of x is 4.