Question

The teacher is standing at Point C, The teachers distance from point A is twice the distance from Point B. what is point C. Point A is at (1,3) and Point B is at (7,6) i culd rlly use this!

Answer 1

C(5,5)

Explanation:

The section formula can be used to find the coordinates of a point (in this case, Point C) that divides a line segment into a given ratio 2:1.

The formula is:

`\sf x = (m \cdot x_2 + n \cdot x_1)/(m + n)`

`\sf y = (m \cdot y_2 + n \cdot y_1)/(m + n)`

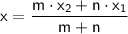
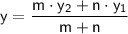
In this formula:

• 
  `\sf (x_1, y_1)` and
  `\sf (x_2, y_2)` are the coordinates of the two given points (A and B in this case).
• 
  `\sf m` and
  `\sf n` are the ratios in which the line segment is divided. In this case, the distance from Point C to Point A is twice the distance from Point C to Point B, so
  `\sf m = 2` and
  `\sf n = 1`.

Now, let's substitute the coordinates of A and B into the formula:

For
`\sf x`:

`\sf x_C = (2 \cdot 7 + 1 \cdot 1)/(2 + 1)`

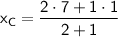
For
`\sf y`:

`\sf y_C = (2 \cdot 6 + 1 \cdot 3)/(2 + 1)`

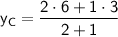
Now, calculate these values:

`\sf x_C = (14 + 1)/(3) = (15)/(3) = 5`

`\sf y_C = (12 + 3)/(3) = (15)/(3) = 5`

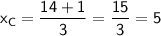
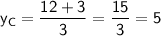
So, the coordinates of Point C are
`\sf (5, 5)`. Therefore, Point C is at (5, 5).