Question

A girl has scored 72, 76, 74, and 75 on her algebra tests.a. Use an inequality to find the score she must make on the final test to pass the course with an average of 78 or higher, given that the final exam counts three testsb. Explain the meaning of the answer to part (a)

Answer 1

Part A.

We know that the final exam counts 3 test. Let x be the score of this final exam, then we can write,

`(72+76+74+75+3* x)/(7)\ge78`

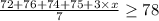
the denominator is 7 because there are 7 scores: 72,76,74,75 and 3 times x (which is the final test). This average must be greater or equal to 78 in order to pass the course.

Then, by adding the numerator terms we get,

`(297+3* x)/(7)\ge78`

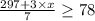
and by moving 7 to the right hand side, we have

`\begin{gathered} 297+3x\ge78*7 \\ or\text{ equivalently} \\ 297+3x\ge546 \end{gathered}`

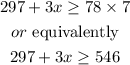
by moving 297 to the right hand side, we obtain

`\begin{gathered} 3x\ge546-297 \\ 3x\ge249 \end{gathered}`

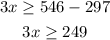
then, the score of the final exam must be

`\begin{gathered} x\ge(249)/(3) \\ x\ge83 \end{gathered}`

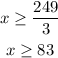
that is, at least greater or equal to 83.

Part B.

The last result means that our girls must obtain at least 83 points in the final test in order to pass Algebra.