Henry's equation with the same solutions as Fiona's
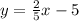 is Option B:
is Option B:
 .
.
Let's start by rewriting Fiona's equation in a more standard form, which is the slope-intercept form y = mx + b, where m is the slope and b is the y-intercept:
Fiona's equation:
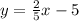
Comparing Fiona's equation with the standard form, we can see that the slope of her equation is
 .
.
For Henry's equation to have all the same solutions as Fiona's, it needs to have the same slope and different constants. Let's check the given options:
Given Options:
A.

B.

C.

D.

Analyzing Henry's Equation:
The slope-intercept form of Henry's equation should have the same slope as Fiona's
 . Let's rearrange the given options to see their slope-intercept forms:
. Let's rearrange the given options to see their slope-intercept forms:
A.
 rearranges to
rearranges to
 . This equation doesn't match Fiona's equation.
. This equation doesn't match Fiona's equation.
B.
 rearranges to
rearranges to
 . This equation matches Fiona's equation.
. This equation matches Fiona's equation.
C.
 rearranges to
rearranges to
 . This equation doesn't match Fiona's equation.
. This equation doesn't match Fiona's equation.
D.
 rearranges to
rearranges to
 . This equation doesn't match Fiona's equation.
. This equation doesn't match Fiona's equation.
Therefore, among the given options, Option B
 represents an equation that has the same solutions as Fiona's equation
represents an equation that has the same solutions as Fiona's equation
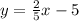 .
.
Question:
Fiona wrote the linear equation
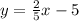 . When Henry wrote his equation they discovered that his equation had all the same Solutions as fionas. which equation could have been Henry's.
. When Henry wrote his equation they discovered that his equation had all the same Solutions as fionas. which equation could have been Henry's.
A.
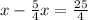
B.
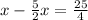
C.
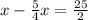
D.
