Question

True or false question …….:……..

Answer 1

Answer: False

Work Shown

`f(\text{x}) = (\text{x}+1)^2-8\\\\\text{y} = (\text{x}+1)^2-8\\\\\text{x}+8 = (\text{y}+1)^2\\\\(\text{y}+1)^2=\text{x}+8 \\\\\text{y}+1=\sqrt{\text{x}+8} \\\\\text{y}=\sqrt{\text{x}+8}-1 \\\\g(\text{x})=\sqrt{\text{x}+8}-1 \\\\`

The +1 at the end should be -1.

To confirm that we have the right inverse, we need to show that
`f(g(\text{x})) = \text{x} \ \text{ and } \ g(f(\text{x})) = \text{x}` are both true for all x in the domain. I'll let the student do these confirmations.

Answer 2

False

Explanation:

To determine if two functions are inverses of each other, we need to verify whether the composition of the functions results in the identity function.

In this case, we will find the inverse of
`\sf f(x)` and check if it is equal to
`\sf g(x)`.

Given function:

`\sf f(x) = (x + 1)^2 - 8` for
`\sf x \geq -1`.

let's find its inverse.

Find
`\sf f^(-1)(x)`:

`\sf f(x) = (x + 1)^2 - 8`

First, swap
`\sf f(x)` and
`\sf x`:

`\sf x = (y + 1)^2 - 8`

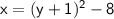
Now, solve for
`\sf y`:

`\sf x + 8 = (y + 1)^2`

`\sf √(x + 8) = y + 1`

`\sf y = √(x + 8) - 1`

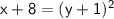
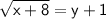
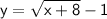
So,
`\sf f^(-1)(x) = √(x + 8) - 1`.

Now, let's check if
`\sf f^(-1)(x) = g(x)`:

`\sf g(x) = √(x + 8) + 1`

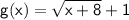
So,
`\sf f^(-1)(x)` is not equal to
`\sf g(x)`, and thus, the functions are not inverses of each other.

Therefore, the answer is False.