Question

50 Points
answer the question as soon as possible

Answer 1

Could Be the Sides of a Right Triangle:

29 in., 20 in., 21 in.

63 in., 16 in., 65 in.

Cannot Be the Sides of a Right Triangle:

4 m, 5 m, 6m

Answer 2

Could Be the sides of a Right Triangle:

• 63 in, 16 in, 65 in
• 29 in, 20 in, 21 in

Cannot Be the sides of a Right Triangle:

• 4 m, 5 m, 6 m

Explanation:

In a right-angled triangle, the Pythagorean theorem must hold, which states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

The Pythagorean theorem is given by:

`\sf c^2 = a^2 + b^2`

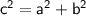
where
`\sf c` is the length of the hypotenuse, and
`\sf a` and
`\sf b` are the lengths of the other two sides.

Let's analyze each set of measurements:

1. Could Be the sides of a Right Triangle:

-
`\sf 63^2 = 16^2 + 65^2` (by the Pythagorean theorem)

Therefore, 63 in, 16 in, 65 in could be the sides of a right-angled triangle.

-
`\sf 29^2 = 20^2 + 21^2` (by the Pythagorean theorem)

Therefore, 20 in, 20 in, 21 in can be the sides of a right-angled triangle.

2. Cannot Be the sides of a Right Triangle:

-
`\sf 4^2 \\eq 5^2 + 6^2` (by the Pythagorean theorem)

Therefore, 4 m, 5 m, 6 m cannot be the sides of a right-angled triangle.