Question

Solve the system of linear equations by substitution.

2x-y=23

x+4y=-20

Answer 1

`\sf x = 8`

`\sf y = -7`

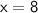
Explanation:

To solve the system of linear equations by substitution, we can isolate one of the variables in one equation and substitute it into the other equation.

Let's solve the first equation for
`\sf x`:

Equation 1:
`\sf 2x - y = 23`

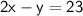
Solve for
`\sf x`

`\sf 2x = y + 23`

`\sf x = (y)/(2) + (23)/(2)`

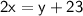
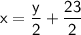
Now we substitute this expression for
`\sf x` into the second equation:

Equation 2:
`\sf x + 4y = -20`

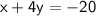
Substitute value of
`\sf x`

`\sf \left( (y)/(2) + (23)/(2) \right) + 4y = -20`

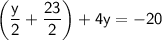
Combine like terms:

`\sf (y)/(2) + (23)/(2) + 4y = -20`

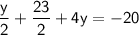
Multiply through by 2 to eliminate the fraction:

`\sf y + 23 + 8y = -40`

Combine like terms:

`\sf 9y + 23 = -40`

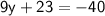
Subtract 23 from both sides:

`\sf 9y + 23 -23= -40 - 23`

`\sf 9y = -63`

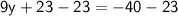
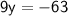
Divide by 9:

`\sf ( 9y)/(9) = -(63)/(9)`

`\sf y = -7`

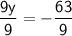
Now that we have the value for
`\sf y`, we can substitute it back into the expression we found for
`\sf x`:

`\sf x = (y)/(2) + (23)/(2)`

`\sf x = (-7)/(2) + (23)/(2)`

`\sf x = (-7 + 23 )/(2)`

`\sf x = (16)/(2)`

`\sf x = 8`

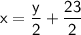
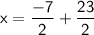
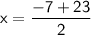
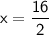
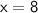
Therefore, the solution to the system of linear equations is
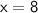`\sf x = 8` and
`\sf y = -7`.