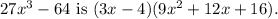Answer:
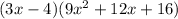
Explanation:
The given expression,
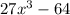 , can be factored using the difference of cubes identity. The difference of cubes identity is given by:
, can be factored using the difference of cubes identity. The difference of cubes identity is given by:
![\[ a^3 - b^3 = (a - b)(a^2 + ab + b^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xsm6hsoqaj1fiz1wjaxjc1ulwwwhiotv88.png)
In this case,
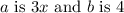 . So, applying the difference of cubes formula, we have:
. So, applying the difference of cubes formula, we have:
![\[ 27x^3 - 64 = (3x - 4)((3x)^2 + (3x)(4) + 4^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bhhg3zz1nsedbhwqmfhhsa6nogztpew56a.png)
Now, simplify the expression:
![\[ 27x^3 - 64 = (3x - 4)(9x^2 + 12x + 16) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/j138mc1w2fyqbhyi4l397r1vsfiq0k67qv.png)
So, the factored form of